Time and Order in Distributed Systems

Breaking down the concept of time in a network of machines

Jun 14, 2025

When working with a distributed system, it is essential to know which of the events happened first. If everything happened on a single machine, then this problem wouldn’t even exist.

But since they work on different machines across the globe, how do we say which of the events happened first?

Problem with `time.Now()`

You probably would have worked with time.Now() , it gives the current Unix epoch time. So why can’t we directly use this?

If we are using clocks, we should be aware that clocks are really difficult to sync. Even if we make it sync properly, it would still be off by some milliseconds or something.

And that millisecond is crucial when it comes to high-throughput systems where events happen instantly.

Let’s look at an example —

Event A occurred on machine M1 at time 10:00:00.100
Event B occurred on machine M2 at time 10:00:00.095

In reality, event B occurred after event A. But the timestamp is earlier due to clock skew or maybe network delays.

So we are clear that using a traditional time.Now() approach wouldn’t work when it comes to these systems. Actually, we don’t care “what time” these events happened; we care about the causality (the order) of events.

So, what to do? Let’s look at some methods designed for this specific problem.

Lamport Clocks

As discussed earlier, we need a way to figure out the order of events happening across machines. So, what if we do the following —

Each process has a local counter (starts at 0).
For every local event, increment the counter → LC = LC + 1
On sending a message, attach the current LC
On receiving a message, update the clock as → LC = max(LC_local,LC_received)+1

Why does this work?

Let’s look at an example. Consider two machines M1 and M2 —

M1 sends a message with LC = 5 to M2.
When M2 receives it, maybe it’s LC = 3.
It sets LC = max(3, 5) + 1 = 6.

From the above interactions —

send event has LC = 5
receive event has LC = 6
→ Causality is preserved: send < receive.

This is what Lamport's clocks say —

If event A happens before event B (A → B), then the logical clock of A is less than that of B: LC(A)<LC(B)

But Lamport clocks fail to determine concurrent events. Let’s understand why —

Suppose:

M1 has LC = 5 and does an event A → LC(A) = 6.
M2 has LC = 2 and does an event B → LC(B) = 3.

Clearly, A and B are independent, with no messages between them.

But - LC(B)=3 < LC(A)=6

So Lamport clocks say B happened before A, but they were concurrent.

Lamport clocks are scalar (single number); two unrelated events on different machines may still get ordered arbitrarily.

So, we got the ordering of events, we just need to figure out how to confidently say if 2 events are concurrent.

Let’s look at another concept to solve this problem.

Vector Clocks

Vector clocks extend what Lamport clocks are built upon. We saw that Lamport clocks were just a single number; the machines only had an idea of their order.

What if we make sure that every machine has an idea of every other machine’s order?

Each machine has a vector:

Length = number of machines N
Each index i in vector → event count from machine M[i]

Why does it work?

Each event carries a snapshot of what that machine knows about everyone else’s state.
On receiving a message, it merges the knowledge using element-wise max.
This way, each machine’s clock contains a partial history of the whole system.

Assume we have N = 3 machines: M0, M1, M2
Each machine maintains a vector VC = [x, y, z]

For every local event, VC[i] += 1
While sending a message, attach our VC
On receiving a message, we merge the incoming VC and our VC, and increment our own VC by 1 -

VC[i] = max(VC[i], VC_msg[i]) for all i

VC[my_index] += 1

Comparing Vector Clocks

Let VC1 and VC2 be two vectors of size N.

1. V1 < V2

To check if VC1 → VC2 (VC1 happened before VC2) we check two things:

Every number in VC1 is less than or equal to the same position in VC2.
(This means VC2 has seen at least everything VC1 has)
At least one number in VC1 is strictly less than in VC2.
(This means VC2 has seen something VC1 hasn’t, so it’s strictly ahead)

If the above holds, → VC1 causally behind VC2.

2. V1 = V2

VC1[i] = VC2[i] for all i

3. V1 and V2 are concurrent

If neither VC1 < VC2 nor VC2 < VC1 → the events are concurrent.

This is the key improvement over Lamport clocks.

I was reading it and I realized, V1 = V2 should have been concurrent, but it’s not. Then what does it signify in the real world?

What does V1 = V2 signify?

It means:
Both events have seen exactly the same number of events from all machines.

So:

They occurred at the same state of the system.
They have the exact same causal history.
Not just concurrent, they are identical in context and causality.

We can imagine two people editing a document:

If they both have seen and made exactly the same edits, their version vectors are equal.
If they each made different edits at the same time without seeing each other’s work, their version vectors are concurrent.

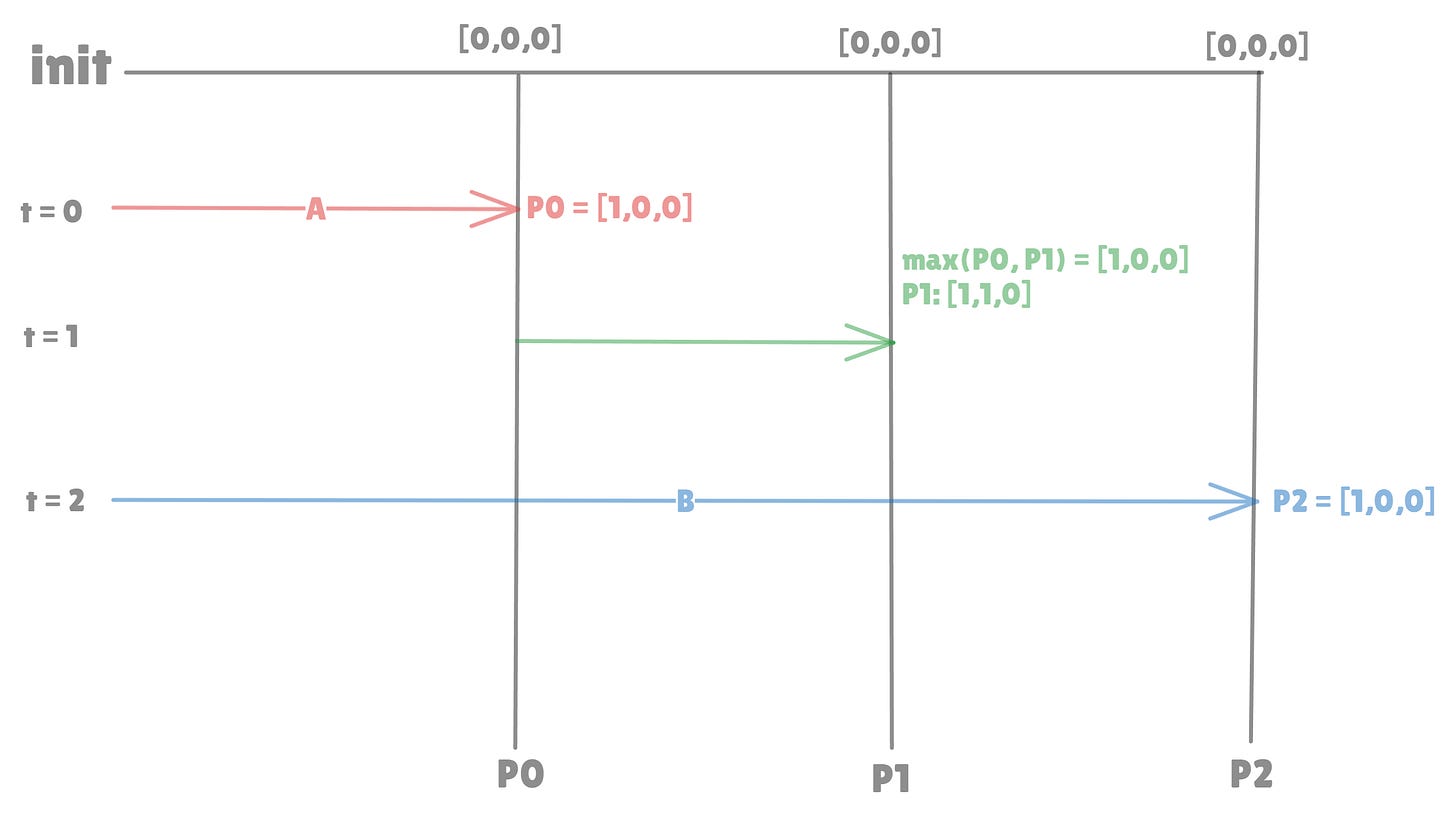
Example

Let:

VC1 = [2, 1, 0]
VC2 = [2, 3, 0]

Compare each index:

VC1[0] = 2 ≤ 2
VC1[1] = 1 ≤ 3 (CORRECT)
VC1[2] = 0 ≤ 0 (CORRECT)
Also, VC1[1] < VC2[1]

So VC1 → VC2 (VC1 causally before VC2)

Let’s take another example —

VC1 = [1, 1, 0]
VC2 = [0, 2, 1]

Now:

VC1[0] > VC2[0] (WRONG)
VC1[1] < VC2[1] (CORRECT)
VC1[2] < VC2[2] (CORRECT)

Mixed results → No full domination

They are concurrent.

The below image might make it clearer —

Drawbacks of vector clocks

Each vector clock has a size proportional to the number of nodes/machines in the system.

If you have N machines, each event's vector clock is of size O(N).
This means every message, every update, or every version tag must carry this vector of size N.

This becomes problematic when:

The number of machines is large (e.g., 1000+ nodes in a distributed database).
You have a lot of messages/events being exchanged frequently.

Thanks for reading Brain Bytes & Binary! This post is public, so feel free to share it.

Real World Applications

Vector clocks are so common that they’re like an integral system of any large-scale application.

1. Dynamo-style Databases (e.g., Amazon DynamoDB, Cassandra)

Problem: Concurrent writes on different nodes with no global order.
Use: Vector clocks tag object versions.
Benefit: Helps detect overwrites vs. concurrent updates for conflict resolution.

2. CRDTs (Conflict-free Replicated Data Types)

Problem: Replicas update independently in eventually consistent systems.
Use: Vector clocks track causality between operations.
Benefit: Enables deterministic conflict resolution.

3. Messaging / Chat Systems

Problem: Simultaneous messages need causal ordering, not just a timestamp.
Use: Vector clocks tell if one message depends on another.
Benefit: Ensures replies appear after the messages they respond to.

4. Real-time Editors (e.g., Google Docs)

Idea: Track which edits (events) each replica has seen.
Use: Conceptually similar to vector clocks for merging changes.
Benefit: Avoids lost updates in collaborative editing tools.

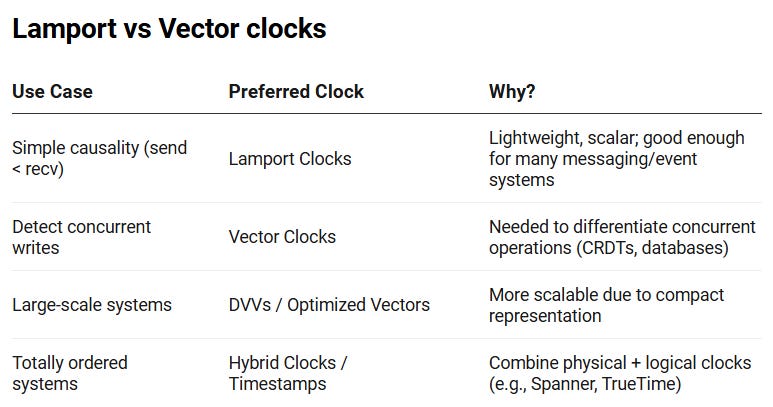
In Brief

Wrapping Up

Time as a concept in physics is fascinating. It’s similar in software engineering.

In distributed systems, it’s not about when events happen, but how they’re related. Lamport clocks help with ordering, but can’t detect concurrency.

Vector clocks address this issue by tracking the causal history.

Depending on the system’s needs, simplicity, accuracy, or scalability, there’s a clock model that fits.

Understanding these concepts helps build systems that remain accurate even in chaotic environments.

That’s all for this week. I will be back with something interesting next week.

Stay tuned!